基于Kalman滤波的经典组合导航中，惯性导航解算(机械编排)充分考虑了地球自转等补偿项的影响。然而，目前基于图优化的组合导航中，IMU预积分(惯导预积分，IMU Preintegration)被设计得比较粗糙，没有考虑地球自转等补偿项的影响，地球自转对IMU预积分性能的影响尚不明确。另一方面，目前MEMS IMU的飞速发展已经使其零偏误差水平接近甚至低于地球自转角速率了，理应在解算中考虑地球自转补偿项，否则就白白浪费了传感器精度！为此，我们采用GNSS/INS组合导航这一简单明了的案例，定量评估了地球自转对MEMS IMU预积分的精度影响，为IMU预积分在图优化定位算法中的合理设计和使用提供了定量参考。

    在基于图优化算法的视觉惯性导航(VINS)算法中，为了有效地引入IMU测量，建立影像帧间相对约束，而又避免每次迭代优化更新后进行重积分，IMU预积分应运而生。然而，采用繁杂的VINS系统很难准确地评估地球自转对IMU预积分的影响，原因有二：1)视觉定位涉及到复杂的参数调整和误差传播，干扰因素多，不利于对预积分性能的明确定量对比评估；2)在视觉系统中，预积分的时长都很短，一般不会超过1秒，地球自转等补偿项的影响很难表现出来。因此，我们采用基于图优化算法的GNSS/INS松组合这一简单清晰的案例来定量评估了地球自转对MEMS IMU预积分的精度影响[1]。具体评估指标采用模拟GNSS短期(60秒)中断期间纯惯导漂移误差的统计曲线，来比较地球自转补偿前后IMU预积分的效果，并与基于传统滤波的GNSS/INS组合导航进行横向对比验证[2]。

    我们采用三组开阔天空环境下的车载数据进行评估。实验中使用了四款不同精度等级的MEMS IMU，它们的零偏不稳定性参数如表1所示。采用我们团队开源的图优化GNSS/INS组合导航软件OB_GINS来评估IMU预积分中补偿地球自转(M2，FGO-Refined)和不补偿地球自转(M3，FGO-Rough)两种情况下的结果。同时也给出传统Kalman滤波的结果作为比照，用M0和M1分别表示补偿和不补偿地球自转的基于滤波的GNSS/INS组合导航结果。

表1：IMU零偏不稳定性参数（Allan方差）

IMU	ICM20602  (InvenSense)	ADIS16460  (ADI)	ADIS16465  (ADI)	HGuide-i300  (Honeywell)
陀螺 (°/h 1σ)	10.0	8.0	2.0	3.0
加表 (mGal 1σ)	30.0	200.0	3.6	20

    图1是四款IMU在四种配置下水平漂移误差随GNSS仿真中断时间的变化曲线。如果不补偿地球自转，无论是传统Kalman滤波组合的惯性导航(M1)还是图优化组合的预积分(M3)都会出现明显的精度下降(即漂移误差更大)，且M1和M3的中断漂移误差表现基本一致。而补偿地球自转后，无论是传统Kalman滤波组合的惯性导航(M0)还是图优化组合的预积分(M2)的精度都有明显改善，IMU器件的精度水平都得以充分发挥，在GNSS中断期间都取得了同样好的推算效果。对比这四款MEMS IMU可以看出，惯性器件精度等级越高，地球自转补偿的影响越显著。在GNSS仿真中断60秒的情况下，在IMU预积分中不补偿地球自转所造成的精度损失为：对于低端消费级MEMS IMU芯片ICM20602，水平定位漂移误差增加了约13%；对于准战术级MEMS IMU模块HGuide-i300，水平定位漂移误差增加了约200%！

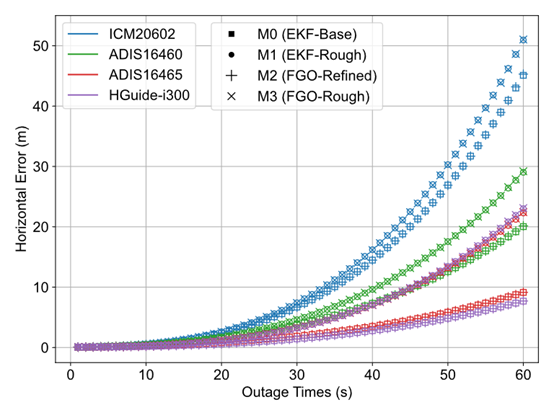
图1：MEMS IMU在不同配置下的GNSS仿真中断水平漂移误差

    结论：在图优化算法中，MEMS IMU预积分往往忽略了地球自转等补偿项，不能充分发挥IMU的精度水平。图优化组合导航中采用补偿地球自转的IMU预积分，能够达到与传统Kalman滤波组合中经典惯导算法同等的精度；反之，会造成显著的精度损失，尤其是针对较高等级(准战术级)MEMS IMU器件。该结论应该同样适用于视觉惯性导航系统(VINS)，尤其是针对复杂场景下视觉退化情形，格外需要考虑MEMS IMU预积分中的地球自转补偿。

    然而，在预积分算法中考虑地球自转补偿项，必须已知IMU的绝对航向(真北)。因此，图优化中的世界坐标系一般要和当地水平坐标系(北-东-地)对齐，需要通过初始航向对准，实现IMU的绝对初始姿态估计。这是IMU预积分补偿地球自转所付出的代价，给它的应用带来了一定的不便。

相关研究细节请阅读参考文献[1]，点击“下载论文全文”。

参考文献：

[1] Tang Hailiang, Zhang Tisheng, Niu Xiaoji, Fan Jing, Liu Jingnan. Impact of the Earth Rotation Compensation on MEMS-IMU Preintegration of Factor Graph Optimization. IEEE Sensors Journal, 2022. DOI:10.1109/JSEN.2022.3192552.  下载论文全文

[2] Zhang Quan, Niu Xiaoji, Zhang Hongping，Shi Chuang. Algorithm Improvement of the Low-End GNSS/INS Systems for Land Vehicles Navigation. Mathematical Problems in Engineering, 2013, 32 (4):1437-1450.  下载论文全文