Allan方差是时频分析和惯性导航领域常用的一种误差分析方法，它有效地刻画了待研究的误差时间序列在不同时间尺度上的波动水平（不稳定性），并可根据不同时间尺度上的Allan方差值所构成的曲线的形状特征来辨识其中包含的随机过程模型。这就类似于我们用功率谱密度（PSD）来描述信号在不同频率尺度上的功率分布，并用PDS曲线来做系统模型辨识。Allan方差分析方法对中长期的随机波动具有很强的表现力，它完全可以作为一个通用的时间序列分析工具来推广到其它应用领域，就像PSD这样的频域分析方法和自相关这样的时域分析方法一样。

 

在我们对惯性导航器件（陀螺和加速度计）进行误差分析时，常采用Allan方差分析方法。这是当初从时频领域（高精度时钟的频率稳定性）借鉴来的一种时间序列分析方法[1]，非常适合于对中长期波动（不稳定性）进行定量描述和分析，因此正是我们惯性器件误差分析所需要的。

与Allan方差相比，传统的误差指标往往是采用误差均值（反映整个误差序列有无宏观偏置）、标准差（反映整个误差序列的波动情况），以及方均根（RMS，可以认为是宏观偏置与波动情况的综合）。如下图所示，它们都是反映误差序列的整体情况的指标，其中含有短时间快速变化和长时间缓变的各个成份，无法细分出不同时间尺度上的误差波动情况。

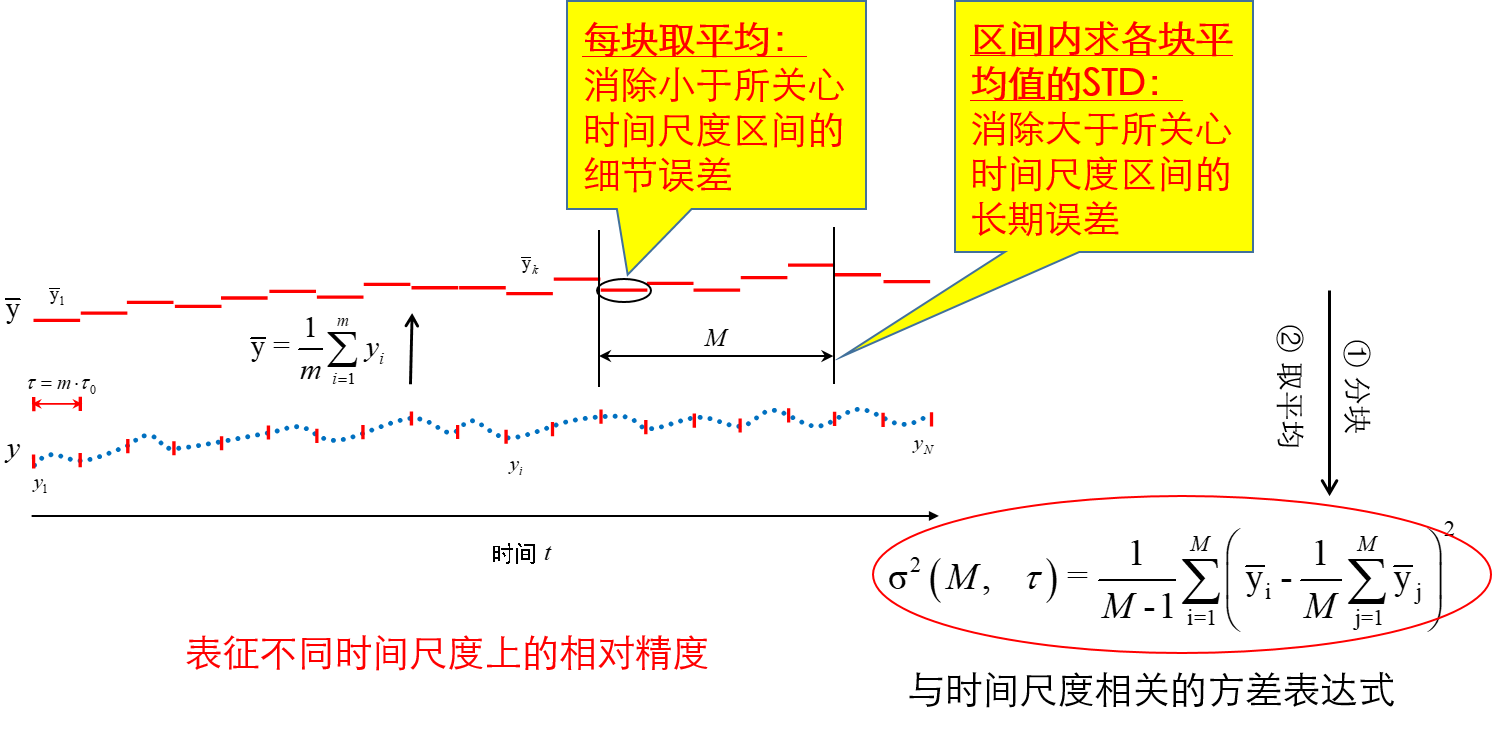
 Allan方差（阿兰方差或阿伦方差）则是将误差序列在某个指定的时间尺度上的波动情况进行了精确提取，其具体计算步骤如下：

1.      将整段误差序列按照你感兴趣的时间尺度的长度（例如1分钟）进行分块；

2.      每块求平均值；

3.      相邻块的平均值求差；

4.      将所有差值进行统计，得到其均方值，并乘以1/2。

这样就得到了对应于这个块长度（1分钟）的Allan方差值。（具体过程见下图）

 

 

这个计算过程看上去有点眼花缭乱，我对Allan方差这样一通操作的理解如下：

如果我们只对某一时间尺度上的误差（即误差波动）感兴趣的话，那么比这个时间尺度更小的细节变化（短时间快速跳动）和比这个时间尺度更大的宏观变化（长时间缓慢漂移）就都不关心了，希望在我们的误差指标中都被消除掉。而Allan方差是这样做到的：

1.      通过分块确定所要考察的时间块长度；

2.      利用块内求平均的办法把短于块长度的那些快速变化成份（细节）都抹掉；

3.      再利用相邻块求差的办法把长于两块长度的那些缓慢变化成份（宏观）都抹掉；

4.      最后对差值序列统计其均方值（这是处理任何随机样本的标准操作），这样统计出来的就是介于1倍块长度和2倍块长度这样一个很窄的时间尺度范围内的误差波动情况。

如果我们对误差序列的各个时间尺度上的成份都感兴趣的话，可以将块长度由短到长，“扫描”一遍，得出一组Allan方差值，然后画个“Allan方差 vs. 块长度”的曲线，这样就能全面反映被研究的误差序列的特性了。具体的，实际上是“Allan方差的开方（Allan Deviation） vs. 块长度”的双对数曲线，以便在更大的范围上有更强的表现力。以下是一张经典的高精度陀螺的Allan方差示意图。

 

 

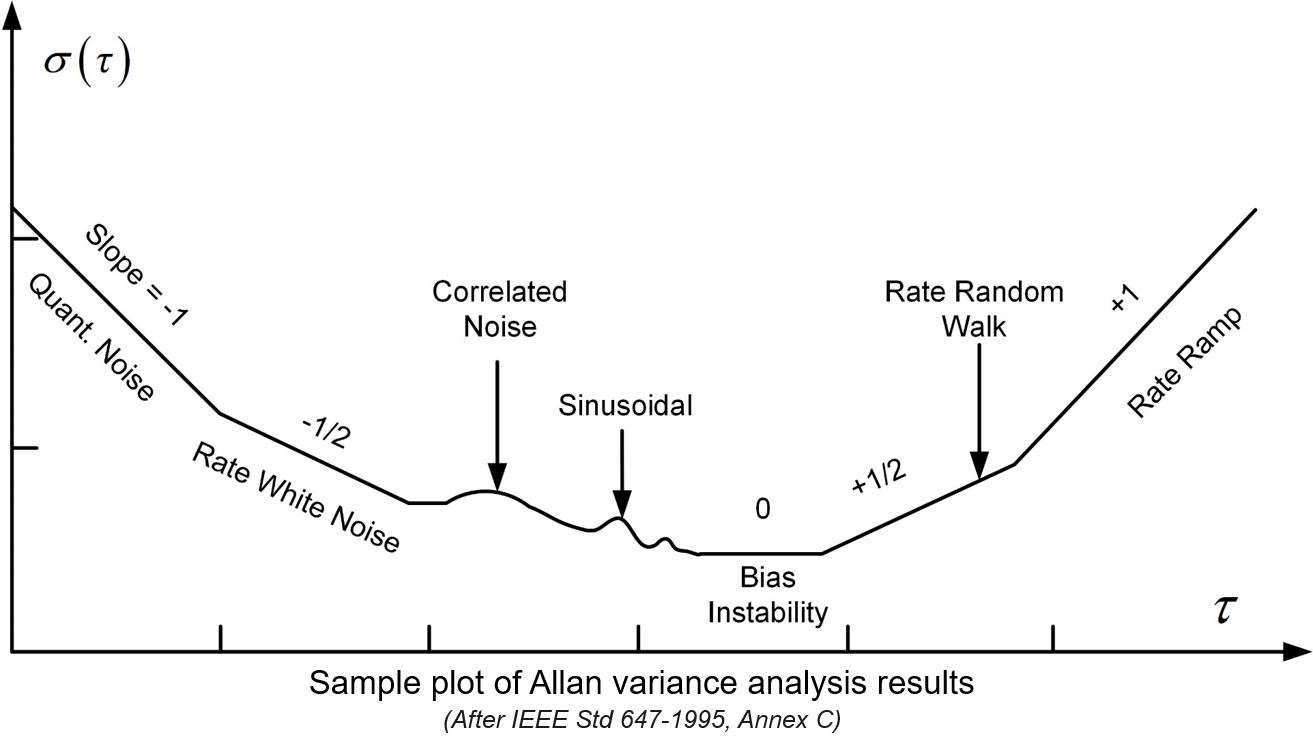
从这根Allan方差曲线上，我们可以根据曲线的形状特征来识别出不同类型的随机误差（即随机过程模型）并提取其参数。例如：斜率为-1/2的直线段代表白噪声。具体可参见IEEE制定的一个关于陀螺测试的技术标准中的附录C内容[2]。这个附录中还给出了一个从Allan方差曲线中分析陀螺的多种随机误差的案例（如上图）。但我想提醒大家，实际的Allan方差曲线往往只能表现出少数两三个主要误差类型，因为其它误差都被这几个主要误差给淹没了。而由于我们在工程上关心的恰恰也就是主要误差源，因此我们并不受此困扰。更多的使用Allan方差分析过程中的注意事项可参考西工大严恭敏老师的博文《Allan方差分析的使用要点》，写得非常精准务实。

大家对Allan方差分析方法的理解可以类比于经典的功率谱密度（PSD）分析方法，只不过后者是描述误差序列在不同频率尺度上的成份，属于频域分析。这两种分析方法对于相同的随机模型是有比较明确的对应关系的，这在那个IEEE标准里也有严谨阐述。

既然如此，为什么我们在已有成熟的功率谱密度分析方法、自相关分析方法等经典的时间序列分析工具之外，还要引入Allan方差呢？我的理解是，PSD和自相关分析都是擅长于分析中短期误差（即中高频成份），而不适用于分析惯导（和时钟）这种看重长期稳定性的传感器。而Allan方差曲线恰恰对中长期时间尺度上的误差特性有很强的表现力。

前文提到了，对应于某个块长度的Allan方差是反映了1~2倍块长度这一狭窄时间尺度范围内的误差成份，那么能否给出一个时间尺度范围更大一些的误差指标，比如能反映1~M倍块长度范围内的误差成份呢？这就涉及到了一类更通用的样本方差分析方法，具体可以参考非常经典的文献[3]。

如下图所示，通用的样本方差分析方法与Allan方差不同之处是在分块、取平均之后，不是采取相邻块求差，而是截取连续M块求其标准方差，然后统计这些标准方差的样本均值，作为反映1~M倍块长度这个时间尺度区间的误差指标。这样就可以灵活地提取和评估我们所关心的任何时间尺度范围内的误差成份！

容易推导，Allan方差只是上述通用样本方差分析在M=2时的一个特例，如下式：

 

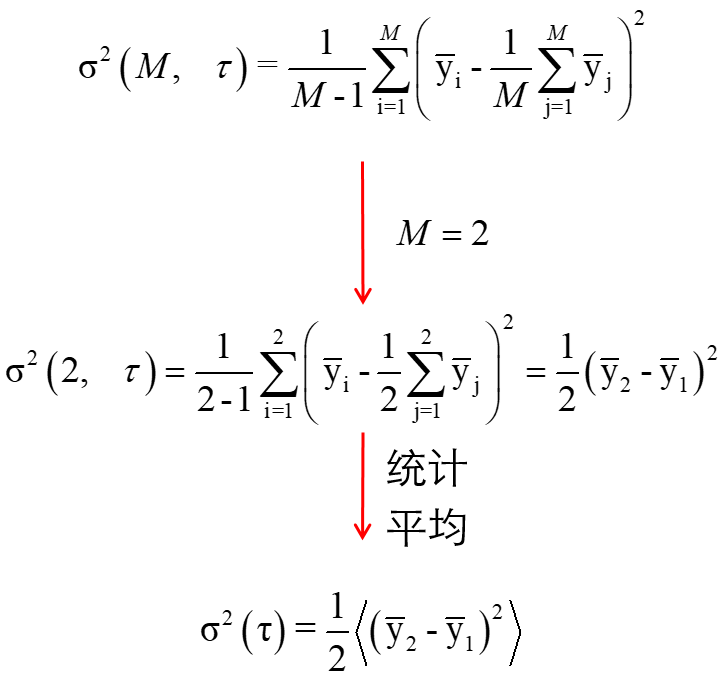
由于Allan方差取M=2这一最小值，因此它具有最高的时间尺度分辨率，对不微附件同时间尺度上的误差成份的刻画最细腻，因此被大家用得最多。

总的来看，Allan方差是一个相对而言直观形象、朴实无华的概念，它当初是在实践中针对高精度时钟稳定性分析的需求而提出的。我相信当我们对某个科研问题日思夜想、废寝忘食的时候，我们脑海中也会自然而然地迸发出类似的概念，来帮助我们解决面临的问题。但基于这种新概念、新指标来形成一套完整自洽的理论体系，则需要扎实的数学功底，不是每个人都能做到的。

理论上讲，Allan方差分析方法并不局限于对惯性器件和时钟误差的分析，也可推广到其它误差序列分析[4~7]；而且它也不局限于是对误差序列进行分析，也可应用于任何时间序列的分析（例如建筑形变、地质演化等）[8]。

本文希望能破除大家对Allan方差的神秘感，将它应用到更广阔的范围里。当然更希望能启发大家在必要时自主提出新的误差指标的定义，来支持自己所在领域的研究。

 

以下为相关参考文献，同时可在研究成果页面访问我们团队关于Allan方差拓展应用于组合导航结果误差分析的相关论文。

[1]   D. W. Allan, Statistics of atomic frequency standards, Proc. IEEE, vol. 54, no. 2, pp. 221–230, Feb. 1966.

[2]  IEEE, IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros, AnnexC, IEEE Std 647-1995, 1995.  IEEE standard for Testing IFOG (Annex C_Allan).pdf

[3]  Riley W J. Handbook of frequency stability analysis [M]. US Department of Commerce, National Instituteof Standards and Technology Gaithersburg, MD, 2008.   Handbook of frequency stability analysis.pdf

[4]  Zhang Q, Niu X, Chen Q, et al. Using Allan variance to evaluate the relative accuracy on different time scales of GNSS/INS systems. Measurement Science and Technology, 2013, 24(8):1659-1666.

[5]  Niu, X., Chen, Q., Zhang, Q.,Zhang, H., Niu, J., Chen, K., ... & Liu, J. (2014). Using Allan variance to analyze the error characteristics of GNSS positioning. GPS Solutions, Volume18, Issue 2 (2014), Page 231-242.

[6]  Zhang Q, Niu X, Shi C. Impact Assessment of Various IMU Error Sources on the Relative Accuracy of the GNSS/INS Systems. IEEE Sensors Journal, 2020, 20(9): 5026-5038.  Impact Assessment of Various IMU Error Sources on the Relative Accuracy of the GNSS_INS Systems.pdf

[7]  张全. GNSS/INS组合导航短期精度的分析方法及应用研究 [D], 2015, 武汉大学.

[8]  Friederichs T . Analysis of geodetic time series using Allan variances [J]. Uni Stuttgart -Universitätsbibliothek, 2010.  (Thomas)Analysis of Geodetic Time Series Using Allan Variance.pdf